import numpy as np
import matplotlib.pyplot as plt
from boreflow import BCArray, Geometry, Simulation, Flux, Limiter, TimeIntegrationSimulating Custom Flow
Example of simulating custom flow on a horizontal surface and a steep slope.
# 1) Create geometry
x = np.array([0, 2, 11]) # X-coordinate x[i]
z = np.array([3, 3, 0]) # Elevation z[i] at x[i]
n = np.array([0.0175, 0.0175]) # Manning roughness (n) between x[i] and x[i+1]
geometry = Geometry(x, z, n)
# Plot the geometry
plt.figure()
plt.plot(x, z, color="black", label="Geometry")
plt.plot([x[0]], [z[0]], "o", color="red", label="Inflow")
plt.plot([x[-1]], [z[-1]], "o", color="blue", label="Free outflow")
plt.legend()
plt.xlabel("x-coordinate [m]")
plt.ylabel("z-coordinate [m]")
plt.axis("equal")
plt.show()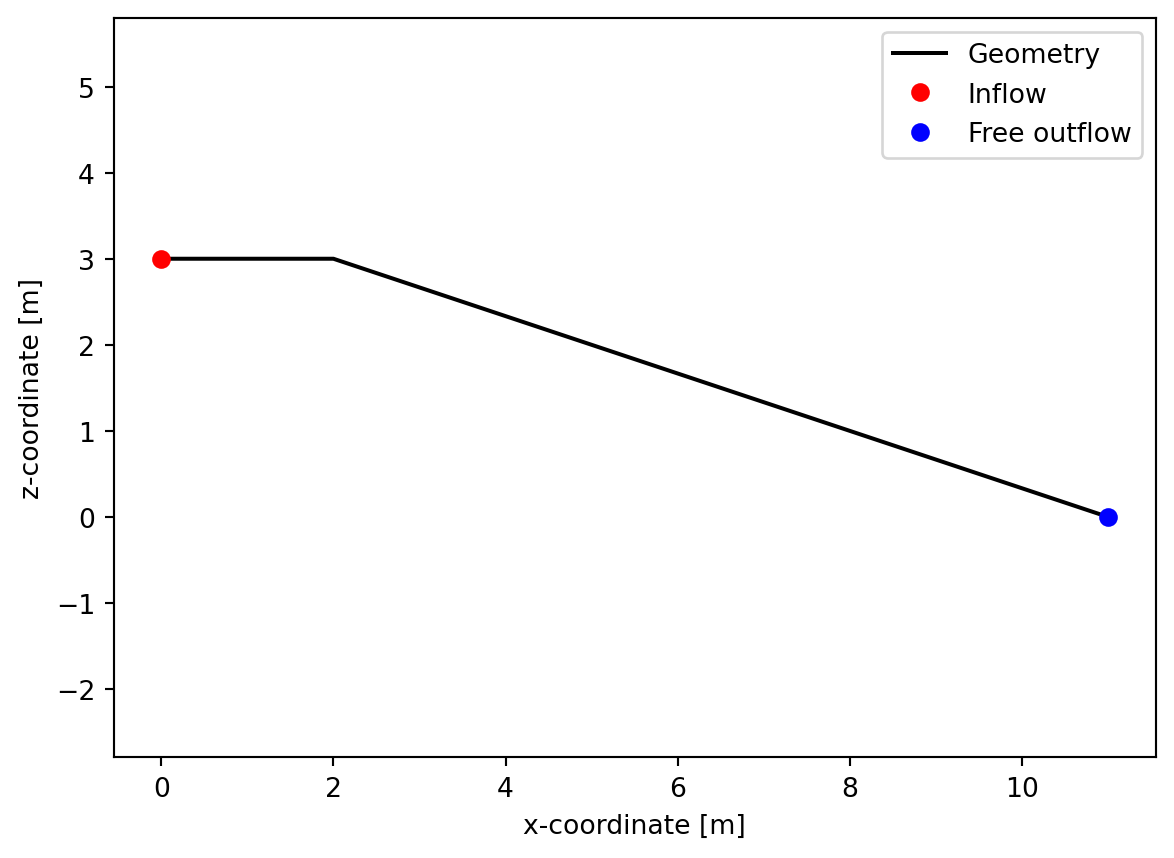
# 2) Create boundary conditions
t = np.array([0, 1, 4])
h = np.array([0.5, 0.8, 0])
u = np.array([1.0, 2.0, 0])
bc = BCArray(t, h, u)
# 3) Initialize simulation settings
sim = Simulation(t_end=10.0, cfl=0.2, max_dt=0.01, nx=110)
# 4) Run the simulation
results = sim.run(geometry, bc, Limiter.minmod, Flux.HLL, TimeIntegration.EF)Simulating: 0%| | 0.00/10.00 sSimulating: 1%|▏ | 0.14/10.00 sSimulating: 3%|▎ | 0.28/10.00 sSimulating: 4%|▍ | 0.41/10.00 sSimulating: 5%|▌ | 0.53/10.00 sSimulating: 6%|▋ | 0.65/10.00 sSimulating: 8%|▊ | 0.77/10.00 sSimulating: 9%|▉ | 0.88/10.00 sSimulating: 10%|▉ | 1.00/10.00 sSimulating: 11%|█ | 1.10/10.00 sSimulating: 12%|█▏ | 1.20/10.00 sSimulating: 13%|█▎ | 1.30/10.00 sSimulating: 14%|█▍ | 1.40/10.00 sSimulating: 15%|█▍ | 1.49/10.00 sSimulating: 16%|█▌ | 1.58/10.00 sSimulating: 17%|█▋ | 1.66/10.00 sSimulating: 17%|█▋ | 1.74/10.00 sSimulating: 18%|█▊ | 1.82/10.00 sSimulating: 19%|█▉ | 1.90/10.00 sSimulating: 20%|█▉ | 1.98/10.00 sSimulating: 20%|██ | 2.05/10.00 sSimulating: 21%|██ | 2.12/10.00 sSimulating: 22%|██▏ | 2.19/10.00 sSimulating: 23%|██▎ | 2.25/10.00 sSimulating: 23%|██▎ | 2.32/10.00 sSimulating: 24%|██▍ | 2.38/10.00 sSimulating: 24%|██▍ | 2.44/10.00 sSimulating: 25%|██▌ | 2.50/10.00 sSimulating: 26%|██▌ | 2.56/10.00 sSimulating: 26%|██▌ | 2.62/10.00 sSimulating: 27%|██▋ | 2.68/10.00 sSimulating: 27%|██▋ | 2.74/10.00 sSimulating: 28%|██▊ | 2.80/10.00 sSimulating: 29%|██▊ | 2.85/10.00 sSimulating: 29%|██▉ | 2.91/10.00 sSimulating: 30%|██▉ | 2.97/10.00 sSimulating: 30%|███ | 3.03/10.00 sSimulating: 31%|███ | 3.09/10.00 sSimulating: 31%|███▏ | 3.14/10.00 sSimulating: 32%|███▏ | 3.20/10.00 sSimulating: 33%|███▎ | 3.26/10.00 sSimulating: 33%|███▎ | 3.32/10.00 sSimulating: 34%|███▍ | 3.38/10.00 sSimulating: 34%|███▍ | 3.44/10.00 sSimulating: 35%|███▌ | 3.50/10.00 sSimulating: 36%|███▌ | 3.56/10.00 sSimulating: 36%|███▌ | 3.62/10.00 sSimulating: 37%|███▋ | 3.69/10.00 sSimulating: 37%|███▋ | 3.75/10.00 sSimulating: 38%|███▊ | 3.81/10.00 sSimulating: 39%|███▉ | 3.88/10.00 sSimulating: 39%|███▉ | 3.94/10.00 sSimulating: 40%|████ | 4.01/10.00 sSimulating: 41%|████ | 4.07/10.00 sSimulating: 41%|████▏ | 4.14/10.00 sSimulating: 42%|████▏ | 4.20/10.00 sSimulating: 43%|████▎ | 4.27/10.00 sSimulating: 43%|████▎ | 4.34/10.00 sSimulating: 44%|████▍ | 4.41/10.00 sSimulating: 45%|████▍ | 4.48/10.00 sSimulating: 46%|████▌ | 4.55/10.00 sSimulating: 46%|████▌ | 4.62/10.00 sSimulating: 47%|████▋ | 4.70/10.00 sSimulating: 48%|████▊ | 4.77/10.00 sSimulating: 48%|████▊ | 4.85/10.00 sSimulating: 49%|████▉ | 4.92/10.00 sSimulating: 50%|█████ | 5.00/10.00 sSimulating: 51%|█████ | 5.08/10.00 sSimulating: 52%|█████▏ | 5.16/10.00 sSimulating: 52%|█████▏ | 5.25/10.00 sSimulating: 53%|█████▎ | 5.33/10.00 sSimulating: 54%|█████▍ | 5.42/10.00 sSimulating: 55%|█████▌ | 5.51/10.00 sSimulating: 56%|█████▌ | 5.60/10.00 sSimulating: 57%|█████▋ | 5.70/10.00 sSimulating: 58%|█████▊ | 5.79/10.00 sSimulating: 59%|█████▉ | 5.89/10.00 sSimulating: 60%|█████▉ | 6.00/10.00 sSimulating: 61%|██████ | 6.10/10.00 sSimulating: 62%|██████▏ | 6.22/10.00 sSimulating: 63%|██████▎ | 6.33/10.00 sSimulating: 64%|██████▍ | 6.45/10.00 sSimulating: 66%|██████▌ | 6.57/10.00 sSimulating: 67%|██████▋ | 6.69/10.00 sSimulating: 68%|██████▊ | 6.83/10.00 sSimulating: 70%|██████▉ | 6.97/10.00 sSimulating: 71%|███████ | 7.11/10.00 sSimulating: 73%|███████▎ | 7.25/10.00 sSimulating: 74%|███████▍ | 7.41/10.00 sSimulating: 76%|███████▌ | 7.56/10.00 sSimulating: 77%|███████▋ | 7.74/10.00 sSimulating: 79%|███████▉ | 7.91/10.00 sSimulating: 81%|████████ | 8.09/10.00 sSimulating: 83%|████████▎ | 8.27/10.00 sSimulating: 85%|████████▍ | 8.47/10.00 sSimulating: 87%|████████▋ | 8.67/10.00 sSimulating: 89%|████████▉ | 8.88/10.00 sSimulating: 91%|█████████ | 9.10/10.00 sSimulating: 93%|█████████▎| 9.32/10.00 sSimulating: 95%|█████████▌| 9.54/10.00 sSimulating: 98%|█████████▊| 9.78/10.00 sSimulating: 100%|██████████| 10.00/10.00 sSimulation done in 10.62 sec# Plot peak flow velocity, peak flow thickness, peak flow discharge
fig, (ax0, ax1, ax2) = plt.subplots(1, 3, figsize=[8, 3.5])
# Mark the transition between the horizontal surface and the sloped surface (x = 2m / s = 2m)
[ax.axvline(2.0, color="grey", ls=":") for ax in [ax0, ax1, ax2]]
# Get results and plot peak flow characteristics
h, u, q = results.get_peak_flow()
ax0.plot(results.s, h, color="black")
ax1.plot(results.s, u, color="black")
ax2.plot(results.s, q, color="black")
# Plot layout
[ax.set_xlabel("Distance (s-coordinate) [m]") for ax in [ax0, ax1, ax2]]
ax0.set_ylabel("Peak flow thickness [m]")
ax1.set_ylabel("Peak depth-avg flow velocity [m/s]")
ax2.set_ylabel("Peak flow discharge [m2/s]")
[ax.set_xlim(0, np.max(results.s)) for ax in [ax0, ax1, ax2]]
[ax.set_ylim(0, None) for ax in [ax0, ax1, ax2]]
fig.suptitle("Peak Flow Characteristics along Geometry")
fig.tight_layout()
plt.show()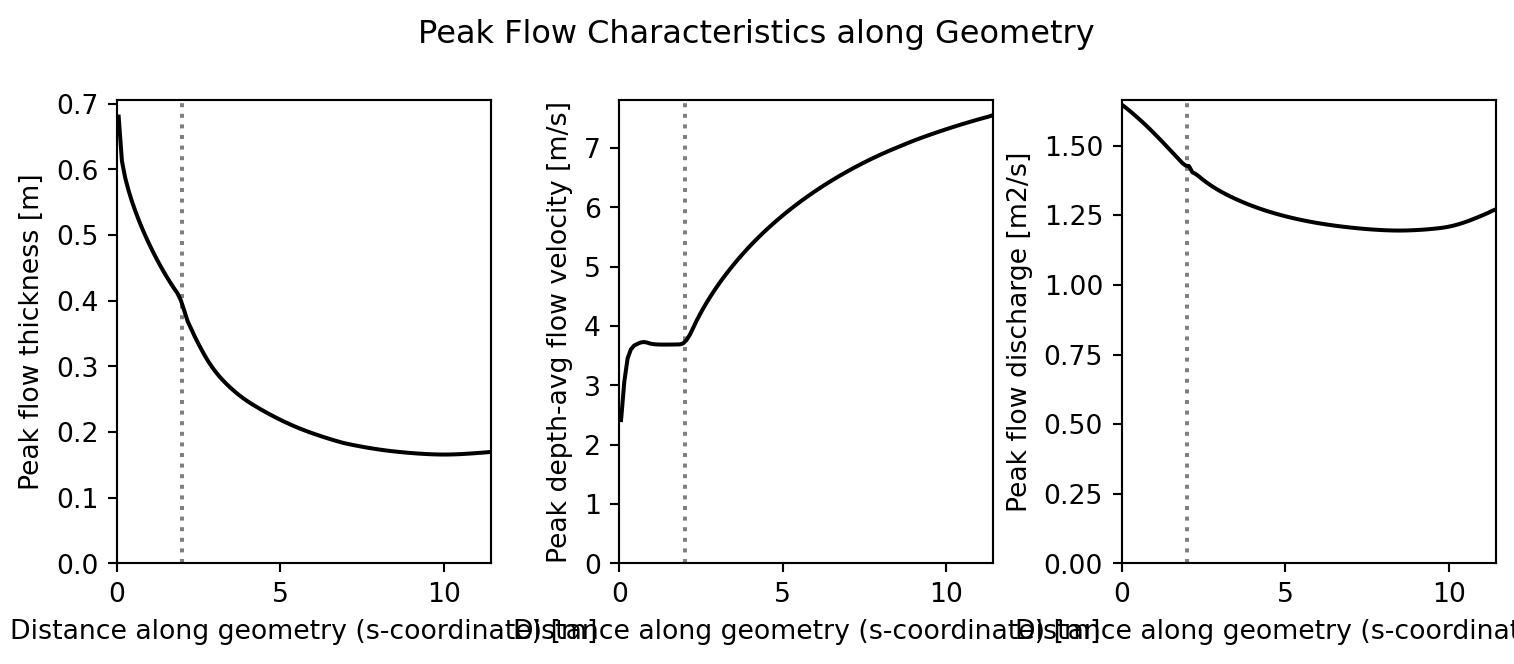
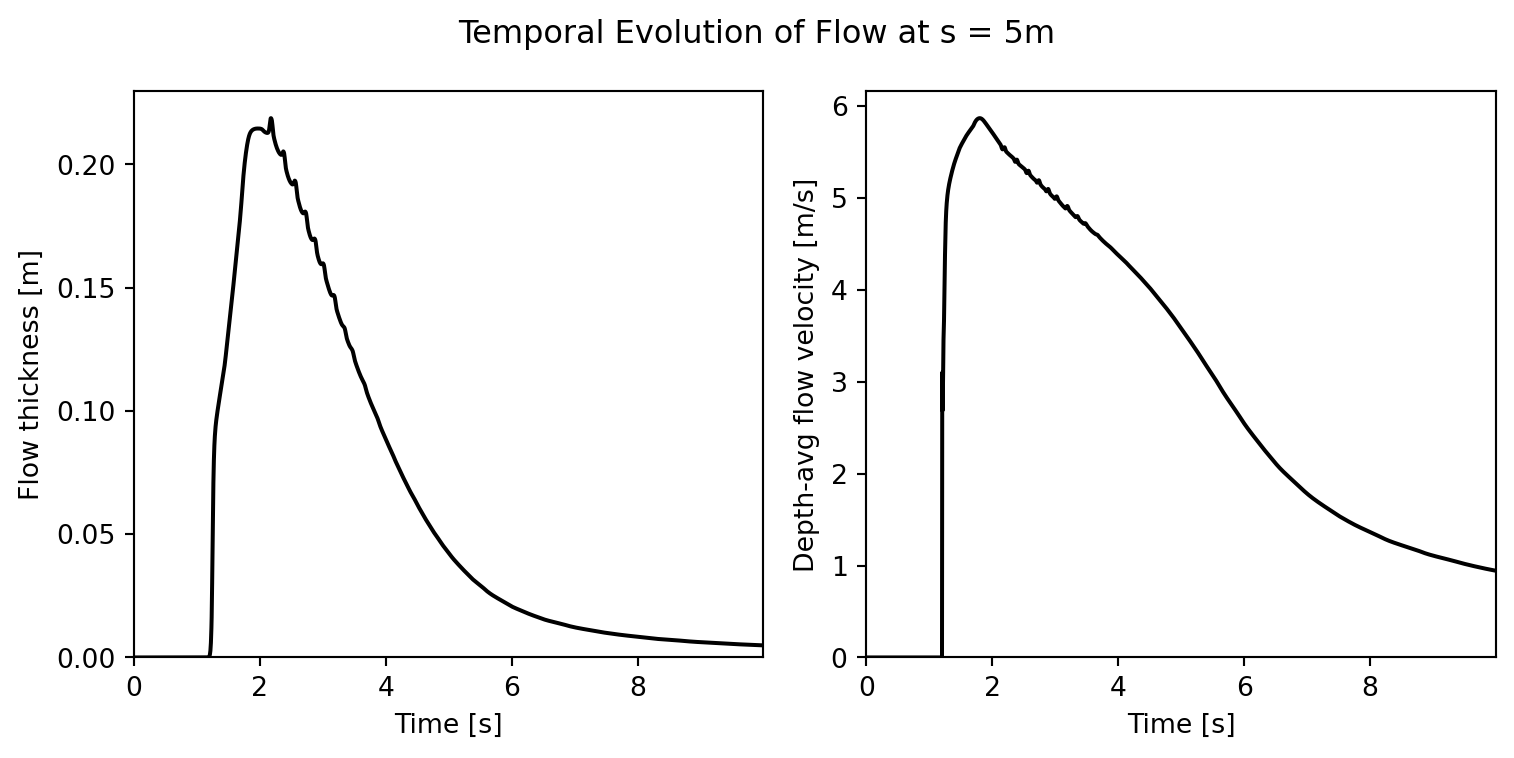
# Plot
fig, (ax0, ax1) = plt.subplots(1, 2, figsize=[8, 4])
# Get and plot the flow at s=5m
res_t, res_h, res_u = results.get_st(s=5.0)
ax0.plot(res_t, res_h, color="black")
ax1.plot(res_t, res_u, color="black")
# Plot layout
[ax.set_xlabel("Time [s]") for ax in [ax0, ax1]]
ax0.set_ylabel("Flow thickness [m]")
ax1.set_ylabel("Depth-avg flow velocity [m/s]")
[ax.set_xlim(0, np.max(res_t)) for ax in [ax0, ax1]]
[ax.set_ylim(0, None) for ax in [ax0, ax1]]
fig.suptitle("Temporal Evolution of Flow at s = 5m")
fig.tight_layout()
plt.show()